The Hardy State is another state that shows predetermined variables can’t reproduce the predictions of quantum theory. This works in a different way than GHZ. It’s not that you can’t find a predetermined setting which isn’t ruled out, but rather that you can get a result that no “legal” predetermined setting could provide.
Details
- hardy
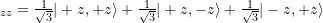
- hardy
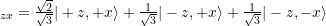
- hardy
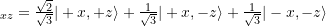
- hardy
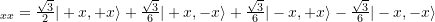
- Unlike the GHZ experiment, it’s easy for Alice and Bob to choose predetermined values which will work for a single experiment. For example, they can just set all their variables to plus.
- It’s simple to show, however, that no predetermined values can reproduce the results of repeated experiments. Just consider the
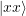 state. If both Alice and Bob do repeated X spin measurements, they will both see spin down (minus) results one out of twelve times.
state. If both Alice and Bob do repeated X spin measurements, they will both see spin down (minus) results one out of twelve times.
- But, when you consider the other three states, there is no way that Alice and Bob can both set their X variables to minus:
az ax bz bx
-- -- -- --
+ - + - +z,-xruled out by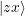
+ - - - +z,-xruled out by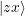
- - + - -x,+zruled out by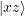
- - - - -z,-zruled out by
Notebooks
-
hardy-state.ipynb
References
- Wikipedia – Search for: Possibilistic nonlocality
This is the version I’m using. - Mermin QC book, Appendix D (p.175 in my copy)
- Nonlocality for Two Particles without Inequalities for Almost All
Entangled States
Lucien Hardy
PHYSICAL REVIEW LETTERS | VOLUME 71, NUMBER 11 | 13 SEPTEMBER 199
(I find the original paper hard to understand.)
